Арксинус, арккосинус, арктангенс и арккотангенс

Ограничения на значения тангенса и арктангенса

Значения тангенса и арктангенса ограничены определенными диапазонами, которые следует учитывать при их использовании. Эти ограничения связаны с особенностями математических функций и их областями определения.

Тангенс — это отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике. Значения тангенса могут быть любыми вещественными числам, кроме некоторых особых значений. Например, для угла 90 градусов (или pi/2 радиан) тангенс не определен, так как в данном случае прилежащий катет равен нулю. Также тангенс может принимать бесконечные значения для углов 90 градусов плюс или минус кратной двум числам.

Арктангенс — это обратная функция тангенса. Значения арктангенса также имеют свои ограничения. Функция арктангенс возвращает угол, для которого тангенс равен заданному значению. Однако она имеет периодичность pi, поэтому значения арктангенса могут быть в интервале от -pi/2 до pi/2 радиан. Также арктангенс может принимать значения бесконечности для значений тангенса, близких к бесконечности.

Тангенс (tg)	Арктангенс (arctg)
От -бесконечности до +бесконечности, кроме некоторых особых значений	От -pi/2 до pi/2 радиан

При использовании тангенса и арктангенса в программировании или математических расчетах необходимо учитывать эти ограничения и проверять входные значения на соответствие. В противном случае, вычисления могут привести к ошибкам или некорректным результатам.

Кнопка MU

«MU» (murk up) — достаточно сложная функция вычисления, которая с английского переводится как «надбавка». С этой кнопкой можно произвести 5 различный операций, каждую из который мы рассмотрим ниже.

Результатом такой операции будет выражение суммы X и Y в процентах от Y. Формула расчета ((X+Y)/ Y)×100.

Тоже самое, что и предыдущая операция, только выражение разницы X и Y в процентах от Y.

К числу Х прибавляет процент от него, который задается значением Y. Формула вычисление будет выглядеть следующим образом: X+Y%, где Y это задаваемое число процента, а сам процент высчитывается от числа X.

Эта формула служит для работы с надбавочной стоимостью. Он применяется, когда нам известен процент, который был взят от некой суммы, но неизвестно значение этой суммы, а только значение этого процента. Например, мы знаем, что мы купили товар со скидкой 20% и его стоимость для нас составила 15 000 руб. И вот мы хотим узнать, какая была изначальная цена без скидки. Тут нам и пригодится кнопка X×Y{MU}.

Набираем на калькуляторе 15 000÷20{MU} и получаем 18 750. Это и есть изначальная стоимость товара. В математическом виде формула расчёта выглядит так: Х÷(1-(Y÷100)).

Это модуль наценки, её абсолютное значение.

Главные значения: arcsin, arccos, arctg и arctg

Применяя таблицы определения значений прямых функций, мы имеем точные числовые значения для следующих углов \ градусов. Таблица является очень простой и понятной для применения при выполнении необходимых расчетов.

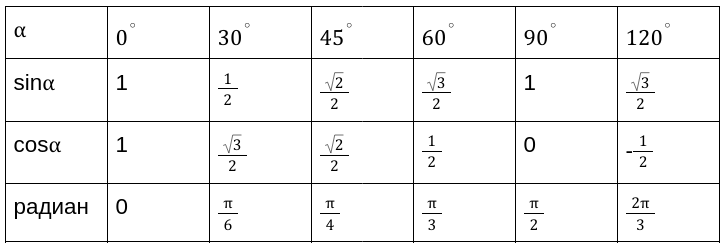
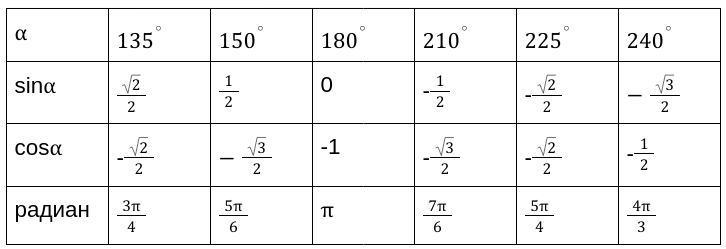Продолжение таблицы 1

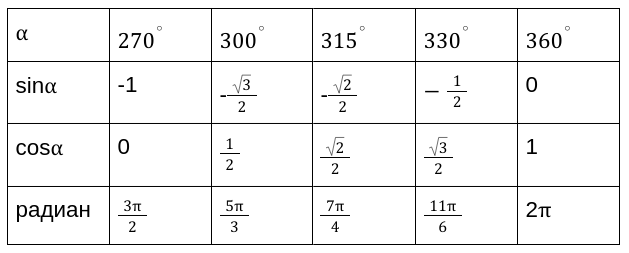
Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более хорошего восприятия.

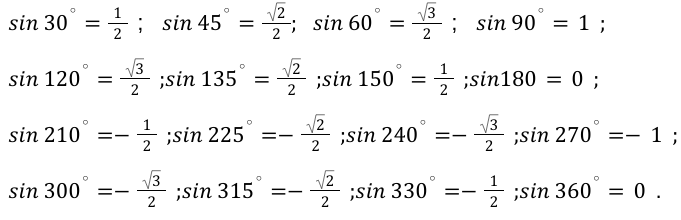
Учитывая данные вышеприведенной таблицы, можно вычислить необходимые для нас значения функций. 

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Для более практичного применения сведем все данные арксинуса в таблицу. Их необходимо запомнить, а лучше всего выучить наизусть. Так ка к ним придется возвращаться на постоянной основе.

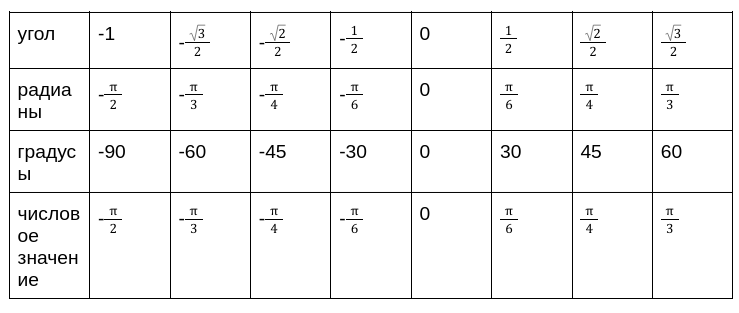
Далее определимся с основными значения арккосинуса. Для вспомнить функцию прямую по значению к данной.

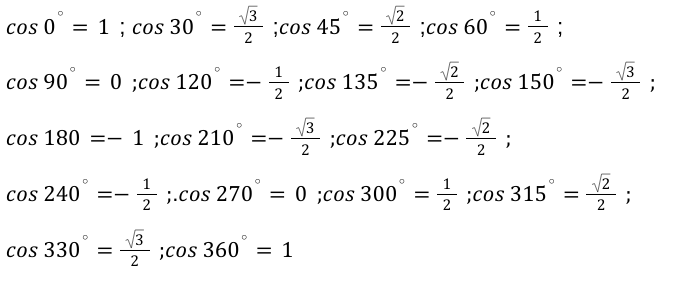
Далее определяем нужные нам значения арккосинуса и сводим их в таблицу.

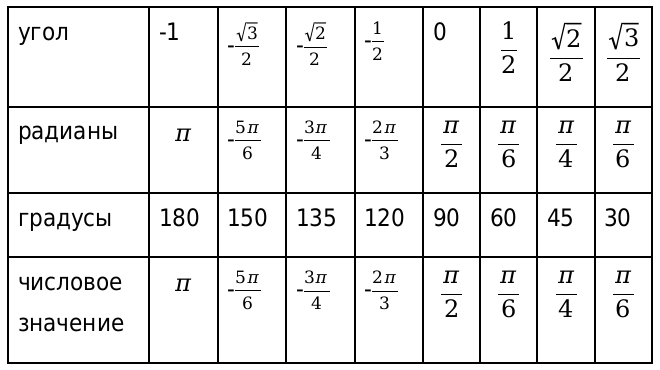
И напоследок остается вычислить значения арктангенса и арккотангенса.

Выведем значения основных прямых функций и получим следующие значения для каждого значения в градусах:

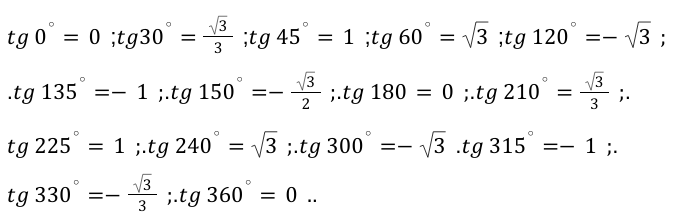
\ — данные угловые значения, не определяются, согласно основным законам геометрии и математики.

\- для перечисленных угловых значений по законам математики и всех технических наук в целом, значения не определяются

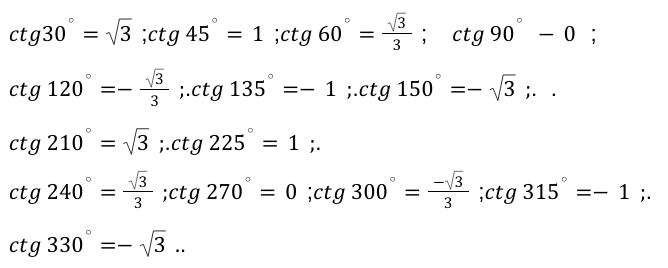
Далее все данные запишем в виде табличной формы.

Первая таблица для арктангенса

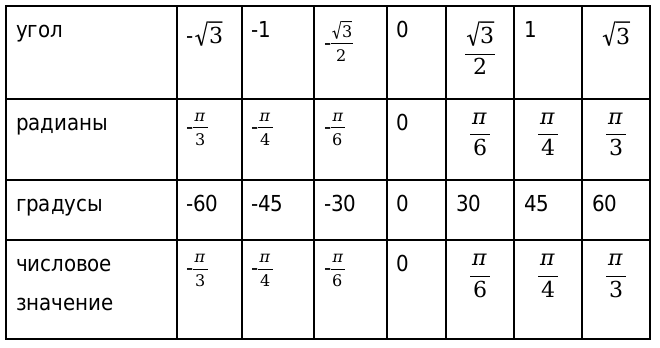
Вторая таблица  для арккотангенса

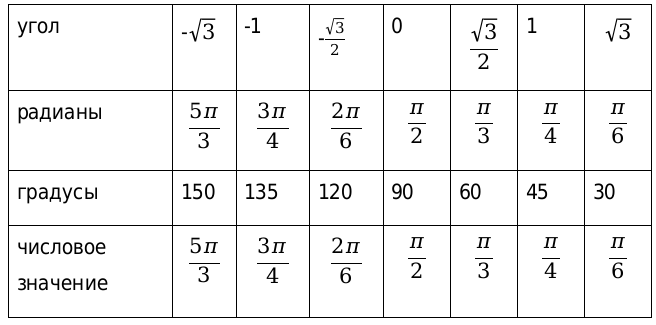
Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.

В данной таблице приведены значения углов, которые считаются нестандартными. Также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе. 

Например:

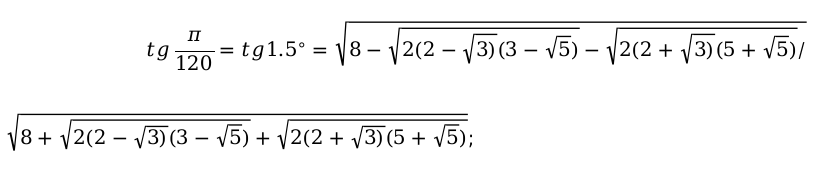
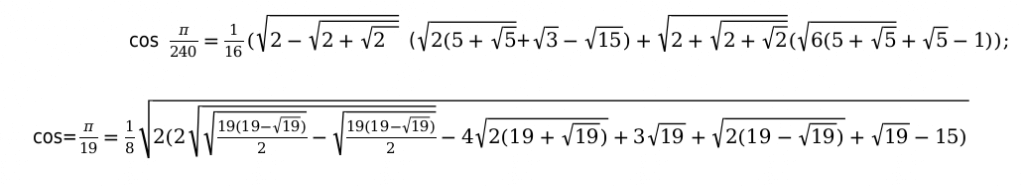
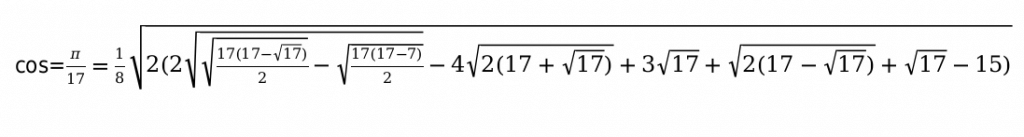
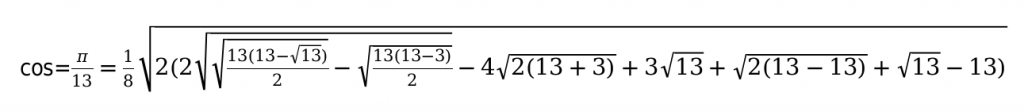
Основные способы, которые помогут заполнить таблицу функций тригонометрии.

Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.

В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее. 

Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции

Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс(sec)

На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух.  Произвести простых четыре перемножения.  

Дважды разделить, умножить и отнять. 

Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме.  

В таблице представлены следующие данные:

• число в квадратной и кубической степени;
• числа квадратных корней;
• логарифмические функции и значение;
• функции тригонометрии, представленный в градусах и радианах;
• обратные функции.

Мы показали, что представляет таблица, какие данные и значения отображает. Полную версию таблицы, можно найти в сборнике. Который издается каждый год. Для определения неизвестных нужно использовать следующие уже известные нам формулы:

\

Пример решения:

Нужно найти значение котангенс 13 градусов 42 минут.  Снова применим таблицу значения функций и найдем значение 13 градусов, а в строке 40 минут и поправку равную 2.  Находим искомое значение 4,102

\

Тригонометрические функции являются периодическими. Функции, которые, являются обратными к ним будут иметь многозначное значение.  Другим словами это множество угловых значений, для которых соответствующая функция является заданным числом.

Арксинус (y = arcsin x )  – это функция, обратная к синусу ( x = sin y ).

Свойства функции	Функции y=arcsin х
E(f)	\
D(f)	\
наличие четности	Нечётная, т.к. arcsin(-x)= — arcsin x
характер графика направление	возрастание

Арккосинус ( y = arccos x )  – это функция, обратная к косинусу ( x = cos y).

Свойства	Функции y=arccos х
E(f)	\
D(f)	\
Чётности	Данное свойство ей не характерно. Иными словами отсутствует.
Монотонность	Убывающая

Арктангенс ( y = arctg x )  – характеризуется, как обратное значение функции относительно тангенса.

Следовательно арккотангенс имеет такие свойства по отношению к тангенсу.

Свойства	y=arctg х	y=arcctg х
E(f)	R	R
D(f)	\	\
Характер функции	Нечётная	Нечётная
Периоды	Возрастающая	Убывающая

Тригонометрический калькулятор онлайн — примеры

Как произвести онлайн расчет синусов и косинусов, тангенсов

Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами. 1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан

1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.

Для включения того или иного режима измерения нажмите нужную кнопку:

где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.

В качестве самого простого примера найдем синус 90 градусов. Нажмите:

90

Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:

60

Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.

Для их ввода необходимо переключить интерфейс, нажав , появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.

Преобразование с кнопкой Dms и Deg на калькуляторе

позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. производит обратный перевод – в формат «градусы; минуты; секунды».

Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:

35,140453 35,23459166666666666666

Переведем в прежний формат: 35,23459166666666666666 35,140453

Десятичный логарифм онлайн

Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:

1

Получается 0 в итоге. Для подсчета lg100 нажмем так:

100

Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.

Так же вычисляется натуральный логарифм, но кнопкой .

Как пользоваться памятью на калькуляторе

Существующие кнопки памяти: M+, M-, MR, MS, MC.

Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.

MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.

Пример. Внесем сто сорок пять в память программы:

145

После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:

На экране отобразится снова 145.

Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем , либо для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой получится 230, а во втором, после нажатия и получится 60.

Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.

Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!

В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.

Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.

Из этой статьи вы узнаете, как пользоваться основными функциями научного (инженерного) калькулятора. Научный калькулятор пригодится при изучении алгебры, геометрии и тригонометрии.

Найдите основные функции. На калькуляторе есть несколько функций, которые понадобятся для решения алгебраических, тригонометрических, геометрических и других задач. Найдите на калькуляторе следующие функции:

Преимущества использования калькулятора Windows для нахождения арктангенса

Калькулятор Windows предлагает ряд преимуществ при использовании для нахождения арктангенса. Вот несколько из них:

1. Удобство использования: Калькулятор Windows предустановлен на большинстве компьютеров с операционной системой Windows, поэтому нет необходимости загружать и устанавливать дополнительное программное обеспечение. Он доступен сразу после запуска и легко открывается одним кликом.

2. Быстрый доступ к функциям: Калькулятор Windows имеет удобный интерфейс, где функции, включая арктангенса, легко доступны всего в нескольких кликах. Пользователь может найти aрктангенс, выбрав вкладку «Научный»

3. Точность вычислений: Как часть операционной системы Windows, калькулятор использует высокоточные вычисления, которые позволяют получать точные результаты для арктангенса

Это особенно важно при решении сложных математических задач

4. Универсальность: Калькулятор Windows поддерживает различные системы счисления, включая десятичную, двоичную, восьмеричную и шестнадцатеричную. Это позволяет легко переключаться между разными системами счисления во время работы с арктангенсом.

5. Доступность калькулятора: Калькулятор Windows можно использовать не только для нахождения арктангенса, но и для других математических операций, включая сложение, вычитание, умножение и деление. Он также поддерживает функции квадратного корня, возведения в степень и многое другое.

6. Надежность: Калькулятор Windows разработан и поддерживается командой Microsoft, что обеспечивает его надежность и актуальность. В случае обновлений и исправлений, пользователь получает все необходимые изменения, чтобы обеспечить более точные и надежные вычисления.

Все эти преимущества делают калькулятор Windows отличным инструментом для нахождения арктангенса и других математических операций. Он является удобным, точным и доступным средством для работы с числами и формулами.

Доказательства формул синусов арккосинуса, арккотангенса и арктангенса

Нужна помощь преподавателя?Опиши задание — и наши эксперты тебе помогут!Описать задание

Для того, чтобы наглядно вывести полученные формулы, нам понадобятся основные тригонометрические тождества и собственно формулы основных обратных функций — косинуса арккосинуса и др. Мы их уже выводили ранее, поэтому тратить время на их доказательства не будем. Начнем сразу с формул синусов арккосинуса, арккотангенса и арктангенса. Используя тождество, получим:

sin2α+cos2α=11+ctg2α=1sin2α

Вспомним, что tgα·ctgα=1. Из этого можно получить:

sinα=1-cos2α, 0≤α≤π sinα=tgα1+tg2α, -π2<><><><>

У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.

Теперь в первой формуле вместо a мы добавим arccos a. Итог — формула синуса арккосинуса.

Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.

Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.

Все наши расчеты можно сформулировать более емко:

sinα=1-cos2α, 0≤α≤π

Следовательно, sin(arccosα)=1-cos2(arccosα)=1-a2

sinα=tgα1+tgα, -π2

Следовательно, sin(arctgα)=tg(arctgα)1+tg2(arctgα)=α1+α2

sinα=11+ctg2α, 0

Следовательно, sin(arctgα)=11+tg2(arctgα)=11+α2

Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.

Их мы выведем по имеющемуся шаблону:

Из cosα=1-sin2α, -π2≤α≤π2 следует, что

cos(arcsin α)=1-sin2(arcsin α)=1-a2

• Из cosα=11+tg2α, -π2<><π2 следует,=»»>
• Из cosα=ctgα1+ctg2α, 0<><>

следует, что cos(arctgα)=ctg(arcctgα)1+ctg2(arcctgα)=α1+α2

Меры углов и тригонометрические функции

Мера угла может быть выражена в градусах (degrees), радианах (radians) или в градах (grads). Соотношение между этими единицами таково $$ 360^\circ=2\pi= 400^g. $$ Один град — это сотая доля прямого угла.

Нажатие кнопки $\stackrel>>$ переключает режимы deg, rad и grad.

В режиме deg введённое число интерпретируется как мера угла в градусах, в режиме rad — в радианах, в режиме grad — в градах. Последовательность $>$ $\stackrel>>$ переводит введённую меру угла в градусы, радианы или грады, и одновременно переключает режимы.

Клавиши $\stackrel^>>$ , $\stackrel^>>$ , $\stackrel^>>$ предназначены для вычисления синуса, косинуса, и тангенса. В режиме deg число на входе интерпретируется этими функциями как значение в градусах, в режиме rad — в радианах, в режиме grad — в градах.

Например, пусть включен режим deg. Тогда результатом команды $$ \fbox \stackrel^>> $$ будет $0.5$. Пусть теперь включен режим rad. Тогда $$ >\ \stackrel> \fbox\ \fbox\ \fbox\ \stackrel^>> $$ тоже даст $0.5$.

Для вызова функций, обратных синусу, косинусу и тангенсу используем последовательности $$ >\ \stackrel^>>, $$ $$ >\ \stackrel^>>, $$ $$ >\ \stackrel^>>. $$ В режиме deg число на выходе этих функций является значением в градусах, в режиме rad — в радианах, в режиме grad — в градах.

Например, пусть включен режим deg. Тогда $$ \fbox\ >\ \stackrel^>> $$ даст 30.

Перевод десятичной дроби в градусах в градусы, минуты, секунды

Для этой цели применяем кнопку $\stackrel>$. Эта функция не зависит от режимов deg, rad и grad.

Чтобы перевести десятичную дробь $A$ (быть может, отрицательную) в градусы, минуты, секунды (Degrees, Minutes, Seconds), вводим $$ A\ >\ \stackrel>. $$ При этом цифры до точки будут обозначать градусы, первая пара цифр после точки — минуты, вторая пара цифр после точки — секунды, третья пара цифр — сотые доли секунды

Обратите внимание на символ $$ \to D.MS. $$

Для перевода меры угла, выраженной в градусах, минутах, секундах в десятичную дробь используем $$ A\ \stackrel>, $$ где во введённом числе $A$ цифры перед точки интерпретируются как градусы, вторая пара цифр после точки — минуты, третья пара цифр после точки — секунды, остальные цифры — десятые, сотые, тысячные и т.д. доли секунды.

Комплекс операций инженерного калькулятора

Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.

Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.

Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.

Ввод цифр производится в двух вариантах:

• с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
• с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами

Примеры применения arctg в геометрии и физике

Функция арктангенса (arctg) широко используется в различных областях математики, в частности в геометрии и физике. Она позволяет решать задачи, связанные с нахождением углов, расстояний и направлений.

Геометрия

В геометрии функция arctg может использоваться для нахождения углов между различными линиями или плоскостями. Например, если известны координаты двух точек P и Q на плоскости, можно найти угол между прямой, проходящей через эти точки, и одной из координатных осей. Для этого нужно вычислить значение arctg отношения разности координат по одной оси к разности координат по другой оси.

Физика

В физике функция arctg применяется для решения задач, связанных с движением и направлением объектов. Например, в задачах динамики можно использовать arctg для определения угла ориентации твердого тела в пространстве. Для этого можно определить отношение проекции вектора ориентации твердого тела на одну из плоскостей к его проекции на другую плоскость и вычислить arctg этого отношения.

Также в физике arctg может применяться для нахождения углов падения и преломления при расчете оптических систем. Например, для определения угла преломления при переходе света из одной среды в другую можно использовать arctg отношения показателей преломления двух сред.

В обоих случаях геометрии и физики, использование функции arctg позволяет получить конкретное числовое значение угла, которое можно использовать для решения практических задач и вычислений.

Нахождение значения аргумента

Например, найдем все значения аргумента, при которых значение функции

На единичной окружности найдем точки
ординаты которых равны 
Этим точкам соответствуют углы 
и
и таких углов бесконечно много. Однако, если рассмотреть промежуток  то на нем функция 
возрастает и принимает все значения от -1 до 1. Поэтому для любого числа
из промежутка 
существует единственное число  такое что
Так на промежутке
существует единственное значение аргумента, при котором значение функции равно  — это угол равный 
( рис.93)

Определение Арксинуса

Этот угол обозначают 
Так,  поскольку  и 

Вычислите:

Решение:

так как 

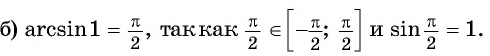
Пример №2

Найдите значение выражения:

Решение:

так как

(рис. 95, б).

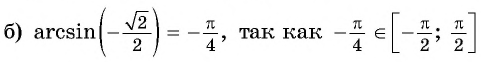
Заметим, что 
( рис.95)  Так как углы, соответствующие точкам
и
где 
с ординатами 
и
отличаются только знаком, то
для любого числа 
(рис. 96).

Пусть 
тогда 
Так как точки
имеют противоположные ординаты, то 
Поскольку  то по определению арксинуса 
Так как  то для любого числа 
Воспользуемся полученным равенством и найдем значение выражения

Так как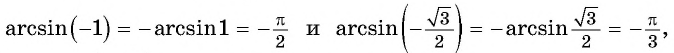 

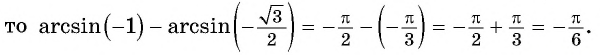
Отметим, что областью определения выражения 
является отрезок  Если 
то выражение не имеет смысла.

Например, выражения  не имеют смысла, так как 
Выражение не имеет смысла, так как 
Из определения арксинуса числа следует, что 
если 

Например,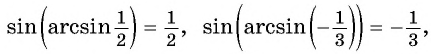 

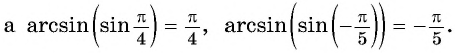
Рассмотрим промежуток  на котором функция 
возрастает и принимает все значения от до 1. Для любого числа  из промежутка 
существует единственное число  такое, что 

Определение Арккосинуса

Этот угол обозначают 

Например:  поскольку 
и 

Вычислите:

Решение:

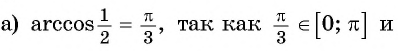
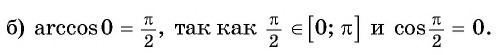
Пример №4

Найдите значение выражения:

Решение:

так как 
( рис. 98.а)

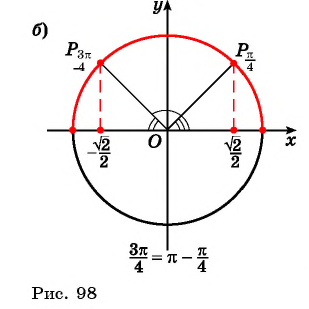
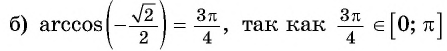
( рис.98.б)

Заметим, что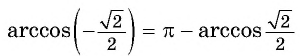 
( см.98)

Пусть 
Так как точки 
имеют противоположные абсциссы, то 
Поскольку то по определению арккосинуса
Так как для любого числа (рис. 99).

Воспользуемся полученным равенством и найдем значение выражения

Так как 
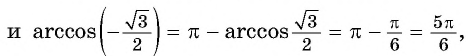
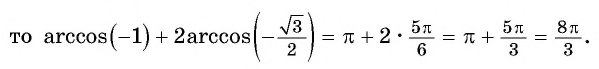
Областью определения выражения  является отрезок 
Если  то выражение не имеет смысла.

Так, выражения
не имеют смысла, поскольку

Выражение 
не имеет смысла, так как 
Из определения арккосинуса числа следует, что
если  и 

Например,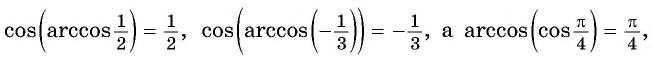 

На промежутке монотонности функции существует единственный угол, тангенс которого равен некоторому данному числу 

Определение Арктангенса

Этот угол обозначают 
Так,  поскольку и 

Вычислите:

Решение:

так как 
и 

и 

Для любого числа 
верно равенство 
(рис. 101).

Пример №6

Найдите значение выражения

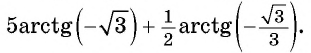
Решение:

Так как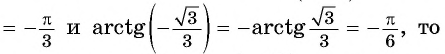 
Из определения арктангенса числа следует, что 
при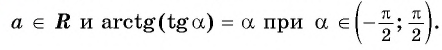 

Например,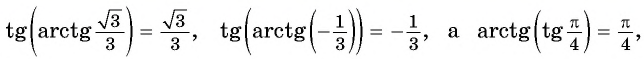 

На промежутке монотонности
функции 
существует единственный угол, котангенс которого равен некоторому данному числу 

Определение Арккотангенса

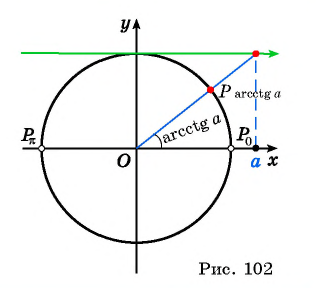
Этот угол обозначают 
Например, поскольку

Вычислите:

Решение:

так как

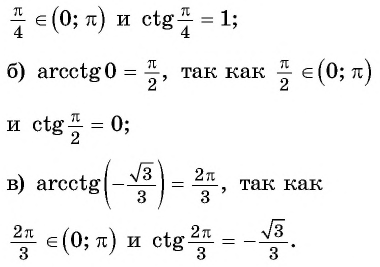
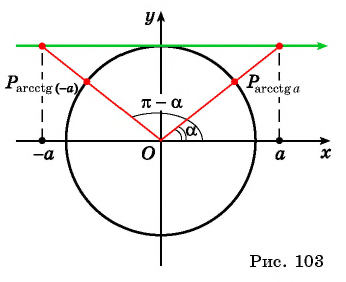
Для любого числа 
верно равенство 
(рис. 103).

Пример №8

Найдите значение выражения 

Решение:

Так как 

Из определения арккотангенса числа следует, что 
если
и 

Например, 

Примеры заданий и их решения

Верно ли, что:

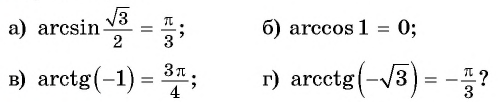
Решение:

• Верно, так как
• верно, так как
• неверно, так как
• неверно, так как

Вычислите:

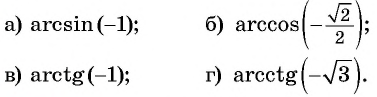
Решение:

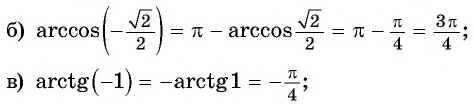
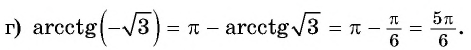
Найдите значение выражения:

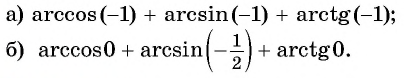
Решение:

Оцените значение выражения 

Решение:

По определению арктангенса числа 

Воспользуемся свойствами числовых неравенств и получим: 

Найдите область определения выражения:

Решение:

• По определению арксинуса числа
  это угол, синус которого равен 
•  По определению арккосинуса числа
  это угол, косинус которого равен 

Найдите значение выражения:

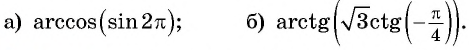
Решение:

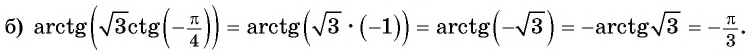
Вычислите 

Решение:

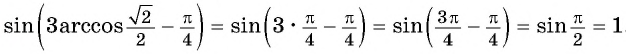
Найдите значение выражения 

Решение:

Воспользуемся формулой
при 
Поскольку 
то эту формулу сразу применить нельзя.

Так как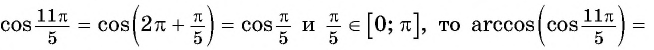 

Возможные путаницы при использовании arctg

При использовании функции arctg (или atan) в математике могут возникать некоторые путаницы, связанные с подходом к углам и их измерению. Рассмотрим некоторые возможные проблемы, которые могут возникнуть при использовании arctg.

1. Единицы измерения угла:

В математике существуют две системы измерения угла: градусы и радианы

В случае функции arctg, обычно используется система измерения в радианах, поэтому важно учитывать, в какой системе измерения указан угол вводимый в arctg

Например, arctg(1) возвращает результат в радианах, что равно примерно 0.7854 радиан или около 45 градусов.

2. Ограничения диапазона:

Значение arctg ограничено определенным диапазоном. В большинстве программных языков обычно возвращается значение от -π/2 до π/2 радиан (от -90 до 90 градусов). Если аргумент arctg находится вне этого диапазона, обычно возвращается значение NaN (Not-a-Number) или бесконечность.

Например, arctg(2) возвращает результат около 1.107 радиан или около 63.4 градусов, тогда как arctg(-2) возвращает примерно -1.107 радиан или около -63.4 градусов.

3. Другие обозначения:

В разных математических текстах и программных языках могут использоваться разные обозначения для функции arctg. Некоторые варианты обозначений включают: atan, arctan, atan2 и т.д

При использовании arctg важно проверить и использовать соответствующее обозначение для вашего языка программирования или математического контекста

Важно принять во внимание эти возможные путаницы, связанные с использованием arctg, чтобы избежать ошибок и получить корректные результаты при выполнении математических вычислений

Установка калькулятора в режим работы с тригонометрическими функциями

1. Включите инженерный калькулятор, нажав кнопку включения.
2. Проверьте, что калькулятор находится в обычном режиме работы. Если необходимо, переключитесь в обычный режим, нажав соответствующую кнопку.
3. Найдите на калькуляторе кнопку с надписью «F» или «2nd». Это кнопка, которая позволяет получить доступ к дополнительным функциям.
4. Нажмите кнопку «F» или «2nd». На дисплее калькулятора должна появиться дополнительная надпись или символ, указывающий на то, что калькулятор находится в режиме работы с дополнительными функциями.
5. Найдите на калькуляторе кнопку с надписью «sin», «cos» или «tan». Это кнопка, которая позволяет вычислить синус, косинус или тангенс угла.
6. Нажмите кнопку «sin», «cos» или «tan». На дисплее калькулятора будет отображаться символ функции, например «sin», а затем введите значение угла.
7. Найдите на калькуляторе кнопку с надписью «x^-1» или «arcsin», «arccos» или «arctan». Это кнопка, которая позволяет вычислить обратную тригонометрическую функцию. Обратная тригонометрическая функция позволяет получить значение угла, зная значение синуса, косинуса или тангенса.
8. Нажмите кнопку «x^-1» или «arcsin», «arccos» или «arctan». На дисплее калькулятора будет отображаться символ функции, например «arcsin», а затем введите значение синуса, косинуса или тангенса.
9. Нажмите кнопку «=» или «Enter» для выполнения вычисления. Результат будет отображен на дисплее калькулятора.

Теперь ваш инженерный калькулятор настроен на работу с тригонометрическими функциями и готов выполнять вычисления арктангенсов и других тригонометрических функций.

Функции инженерного калькулятора

Калькулятор умеет работать со степенями и логарифмами. Находит синус, косинус, тангенс и котангенс, а также арксинус, арккосинус, арктангенс и арккотангенс. Поддерживает двоичные логарифмы, логарифмы по основанию. Может возвести число в 10-ю степень. Также, калькулятор позволяет просматривать число Эйлера и число Пи. Помимо этого поддерживаются стандартные арифметический действия, с помощью которых вы можете сложить и вычесть числа, умножить и разделить, а также извлечь квадратный корень онлайн.

Подробная инструкция и ознакомление с основными возможностями.

1. Найти корень. Чтобы найти квадратный корень числа, введите это число в калькулятор, а затем нажмите кнопку «√», которая находится в верхнем ряду основного блока, вторая справа. Допустим, если мы введем число 9, то после нажатия на эту кнопку получим число 3.
2. Возвести число в квадрат. Чтобы возвести число в квадрат онлайн вам необходимо воспользоваться кнопкой «X2», которая находится в левом блоке функций, в правой части третьего ряда снизу. В результате число, имевшееся на экране, будет возведено в квадрат. К примеру, на экране горит 3. В результате мы получим 9.
3. Возвести число в степень. Возвести число в степень можно с помощью кнопки «Xy» в правом верхнем углу калькулятора. Сначала введите число, которое нужно возвести, затем нажмите на эту кнопку и введите число самой степени. Например, если мы попробуем возвести 10 в степень 2, то получим 100.
4. Синус, косинус, тангенс, котангенс. Часто бывает так, что необходимо найти синус острого угла, косинус прямого угла, синус внешнего угла, а также тангенс или котангенс треугольника. На нашем калькуляторе данные вычисления можно производить с помощью кнопок «sin», «cos», «tg», «ctg». Приведем конкретный пример: допустим, нам требуется найти косинус угла в 90 градусов. Для этого, введем на калькуляторе цифру 90 и нажмем кнопку «cos» в левом блоке функций. В результате мы получим длинную цифру -0.4480736161291701. Это и есть косинус угла 90. Точно так же на нашем калькуляторе можно вычислить косинус угла 60, синус угла 90 и многое другое.
5. Арксинус арккосинус арктангенс арккотангенс. Вычисляются точно так же как и в предыдущем примере. Просто введите нужное число (градусы угла) и нажмите на одну из следующих кнопок соответственно: «asin», «acos», «atg», «actg».
6. Логарифм по основанию вычисляется с помощью кнопки logyx. Введите число, допустим 10. Затем нажмите на эту кнопку и введите основание. Допустим 2. После нажатия на кнопку равно, мы получим ответ: 3.321928094887.
7. Возвести 10 в n-ю степень. С помощью данной функции можно возвести число 10 в степень, которая горит на табло калькулятора. Для этого используем кнопку X2,  которая располагается во втором ряду снизу (в левом блоке). К примеру, у нас на экране горит цифра 2. В результате произойдет возведение 10 во 2-у степень, т.е. 10^2=100.
8. Превратить число в отрицательное или положительное. Иногда требуется превратить число в отрицательное или наоборот. Чтобы не вводить его заново, просто нажмите на кнопку «+/-»
9. Посмотреть число Пи и число Эйлера можно с помощью кнопок «П» и «е» в правом углу левого блока.
10. Простые математические действия осуществляются с помощью клавиш в правом (основном) блоке. «+» — сложение, «-» — вычитание, «x» – умножение и «÷» — умножение.
11. Функция памяти. Пользоваться функцией памяти в нашем онлайн калькуляторе очень просто. Допустим, вы получили какое-то число, которое нужно запомнить. Чтобы сделать это нажмите «M+». Когда это число вам понадобится, просто нажмите кнопку «MR» и оно выведется на экран. После этого вы сможете совершать с ним математические операции. Также, вы можете плюсовать или вычитать имеющееся число из числа, которое уже в памяти. Допустим, в памяти у вас число 10. А на экране число 2. Если вы нажмете кнопку «M-«, то из 10 вычтется 2 и в памяти останется число 8. Точно так же происходит с кнопкой «M+». Если вы хотите очистить память — нажмите «MC» и память станет пустой.
12. Разделить целое на текущее. Часто в инженерной работе требуется провести довольно тривиальное вычисление: узнать, сколько текущий показатель составляет от единого целого. Для этого в нашем инженерном калькулятор существует кнопочка 1/x. Она делит единицу на текущее число. Скажем, если на табло горит 5, то функция выведет 0.2.

Подводя итоги: арктангенс в калькуляторе Windows — быстрый и удобный способ нахождения

В статье мы подробно рассмотрели процесс нахождения арктангенса с помощью калькулятора Windows. Как вы могли убедиться, этот метод оказывается очень простым и выгодным, особенно для тех, кто работает с Windows операционной системой.

Главное преимущество использования арктангенса в калькуляторе Windows заключается в том, что вы не нуждаетесь в дополнительных инструментах или математическом образовании. Все, что вам понадобится — это открыть калькулятор и следовать инструкциям, которые мы предоставили в статье.

Кроме того, калькулятор Windows позволяет вам работать с арктангенсом на различных устройствах, таких как персональные компьютеры и ноутбуки, что делает его доступным для широкой аудитории пользователей.

В заключение, использование арктангенса в калькуляторе Windows — это удобный и эффективный способ нахождения арктангенса. Он позволяет вам быстро получить необходимый результат без лишних усилий и затрат времени на ручные расчеты.

Преимущества	Недостатки
Простота использования	Требует наличия Windows операционной системы
Не требует математического образования	Доступен только на устройствах с Windows
Доступность для широкой аудитории пользователей
Быстрое получение результатов

В целом, использование арктангенса в калькуляторе Windows является наиболее удобным и эффективным способом для нахождения этой тригонометрической функции. Мы рекомендуем вам использовать этот метод, если вам требуется быстро и точно рассчитать арктангенс.